Три закона Кеплера (эллипсов, площадей, гармонический)

Предположение о равномерном круговом движении планет Солнечной системы не согласовывалось с гелиоцентрической системой мира Н. Коперника, поскольку расхождения между вычисленным и реальным положением планет в определённые промежутки времени было значительным. Это противоречие удалось разрешить выдающемуся немецкому астроному И. Кеплеру. На основании многолетних наблюдений за движением планет, изучения трудов своих предшественников Кеплер открыл три закона, названных впоследствии его именем.

Первый закон Кеплера, называемый также законом эллипсов, был сформулирован учёным в 1609 г.

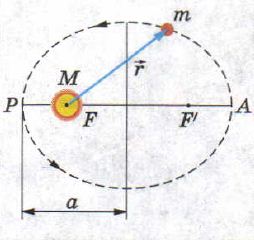
Первый закон Кеплера: все планеты Солнечной системы движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.

Ближайшая к Солнцу точка P траектории называется перигелием, точка A, наиболее удалённая от Солнца, — афелием. Расстояние между афелием и перигелием составляет большую ось эллиптической орбиты. Половина длины большой оси, полуось a, — это среднее расстояние от планеты до Солнца.

Среднее расстояние от Земли до Солнца называется астрономической единицей (а. е.) и равно 150 млн км.

Форму эллипса, степень его отличия от окружности определяет соотношение c/a, где c — расстояние от центра эллипса до фокуса, a — большая полуось эллипса.

Чем больше это отношение, тем более вытянута орбита движения планеты (рис. 37), фокусы находятся дальше друг от друга. Если это отношение равно нулю, то эллипс превращается в окружность, фокусы сливаются в одну точку — центр окружности.

Орбиты Земли и Венеры почти круговые, для Земли соотношение c/a составляет 0,0167, для Венеры — 0,0068. Орбиты других планет более сплющенные. Наиболее вытянута орбита Плутона, для которого c/a = 0,2488. По эллиптическим орбитам движутся не только планеты вокруг Солнца, но и спутники (естественные и искусственные) вокруг планет. Ближайшая к Земле точка движения спутника называется перигеем, самая удалённая — апогеем.

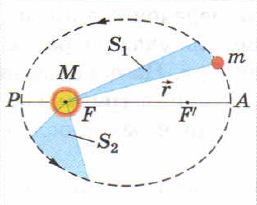
Рис. 37. Схема эллиптической орбиты движения планет: P — перигелий; A — афелий; a — среднее расстояние от планеты до Солнца; m — масса планеты; M— масса Солнца; F, F' — фокусы орбиты; r — радиус-вектор планеты

Рис. 38. Схема движения планет вокруг Солнца в равные промежутки времени: P — перигелий; A — афелий; m — масса планеты; M — масса Солнца; r — радиус- вектор планеты; S1, S2 — площади, описываемые радиусом- вектором планеты; F, F' — фокусы орбиты

Второй закон Кеплера (закон площадей): радиус-вектор планеты описывает в равные промежутки времени равные площади.

Загрузка...

На рисунке 38 проиллюстрирован второй закон Кеплера. Из рисунка понятно, что радиус-вектор — это отрезок, соединяющий фокус орбиты (по сути, центр Солнца) и центр планеты в любой точке её движения по орбите. В соответствии со вторым законом Кеплера площади выделенных цветом секторов равны между собой. Тогда получается, что за одинаковый промежуток времени планета проходит по орбите разное расстояние, т. е. скорость движения не постоянна: v₂ > v₁. Чем ближе планета к перигелию, тем быстрее её движение, будто она стремится скорее уйти подальше от палящих солнечных лучей. Материал с сайта http://doklad-referat.com

Третий закон Кеплера (гармонический): квадраты периодов обращения двух планет вокруг Солнца относятся друг к другу, как кубы больших полуосей их орбит.

Помня, что длина большой полуоси орбиты считается средним расстоянием от планеты до Солнца, запишем математическое выражение третьего закона Кеплера:

T²₁ / T²₂ = a³₁ / a³₂,

где T₁, T₂ — периоды обращения планет 1 и 2; a₁ > a₂ — среднее расстояние от планет 1 и 2 до Солнца.

Третий закон Кеплера выполняется как для планет, так и для спутников, с погрешностью не более 1 %.

На основании этого закона можно вычислить продолжительность года (время полного оборота вокруг Солнца) любой планеты, если известно её расстояние до Солнца. И наоборот — по этому же закону можно рассчитать орбиту, зная период обращения.